I have been preparing a multiple choice test for our Racket course. The test will consist of 30 questions, each of which has 4 options and only one of them is the correct answer. Students will need to answer to at least 15 questions to pass the test.
Where are these numbers coming from? Why 15 out of 30 and not 12 (40%)? Why 4 options and not 2, with a true/false option only? More importantly: how many questions will be answered correctly by someone selecting random answers?
Let’s suppose that a student is answering randomly. What is the probability that the student answers all questions in the wrong way? This is not difficult to compute: in our case this is ![]() . What about one right and 29 wrong? This is
. What about one right and 29 wrong? This is ![]() multiplied by
multiplied by ![]() , but you should also remember that there are 30 different ways to get a question right (it could be the first or the second or … or the thirtieth). So, overall, the probability of getting 1 question right and 29 wrong is
, but you should also remember that there are 30 different ways to get a question right (it could be the first or the second or … or the thirtieth). So, overall, the probability of getting 1 question right and 29 wrong is ![]() . This is nearly ten times more likely than getting all the questions wrong.
. This is nearly ten times more likely than getting all the questions wrong.
In general, what is the probability of getting ![]() questions right and 30-
questions right and 30-![]() wrong? This is
wrong? This is ![]() , but we should also multiply this number by the possible combinations of n elements out of 30, that is:
, but we should also multiply this number by the possible combinations of n elements out of 30, that is:
![]()
The following is a plot of this function:
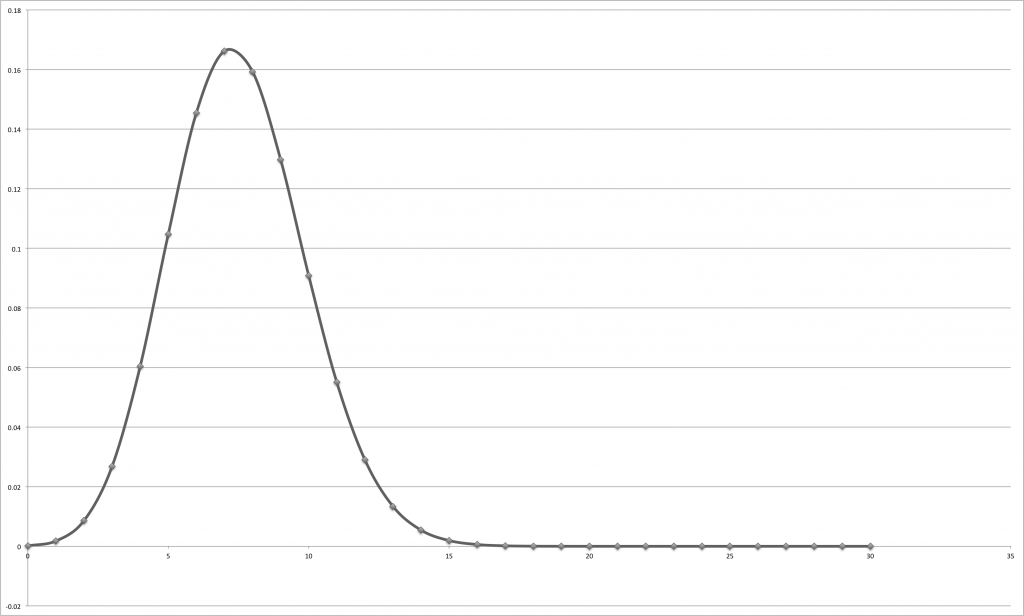 As you can see this function has a peak for n=6; the average is
As you can see this function has a peak for n=6; the average is ![]() . So, on average, a “random answerer” would get 7.5 questions right. What is the probability of passing the test by answering randomly? We need a cumulative function for this. Let’s plot the probability of passing a test where it is required to answer
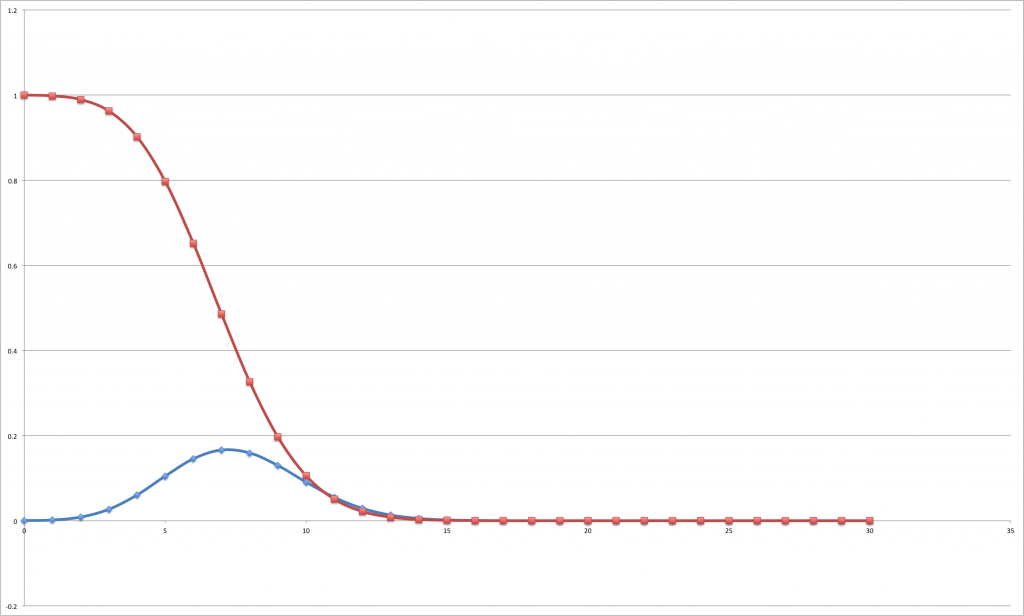
. So, on average, a “random answerer” would get 7.5 questions right. What is the probability of passing the test by answering randomly? We need a cumulative function for this. Let’s plot the probability of passing a test where it is required to answer ![]() questions correctly out of 30 (this is the line in red; the blue line is
questions correctly out of 30 (this is the line in red; the blue line is ![]() as defined above):
as defined above):
The probability is obviously 1 if no correct answers are required, and then it decreases reaching 0.001 for ![]() . Going back to the original question: the probability that a student answering randomly passes the test is 0.1%.
. Going back to the original question: the probability that a student answering randomly passes the test is 0.1%.
[Thanks to Lorenzo Gheri for his input on this :-)]